Local search algorithms turn out to be effective in solving many CSPs. They use a complete-state formulation: the initial state assigns a value to every variable, and the search changes the value of one variable at a time.

For example, in the 8-Queen problem, the initial state might be a random configuration of 8 Queens in 8 columns, and each step moves a single queen to a new position its column.

Typically, the initial gauss violets several constraints. The point of local search is to eliminate the violated constraints. In choosing a new value for a variable, the most obvious heuristic is to select the value that results in the minimum number of conflicts with other variables the min-conflicts heuristic.

The algorithm is shown in figure 1 and its application to an 8-queens problem is diagrammed in figure 2.

function MIN-CONFLICTS(csp, max_steps) returns a solution or failure
    inputs: csp a constraint satisfaction problem
        max_steps, the number of steps allowed before giving up
    current ← an initial complete assignment for csp
    for i = 1 to max_steps do
        if current is a solution for csp then return current
        var ← a randomly choosen conflicted variable from csp. VARIABLES
        value ← the value v for var minimizes Conflicts (var, v, current, csp)
        set var = value in current
    return failure

[Figure – 1]

Figure 1: The MIN-CONFLICTS algorithm for solving CSPs by local search. The initial state may be choosen randomly or by a greedy assignment process that chooses a minimal conflict value for each variable in turn. The CONFLICTS function counts the number of constraints violated by a particullar value, given the rest of the current assignment.

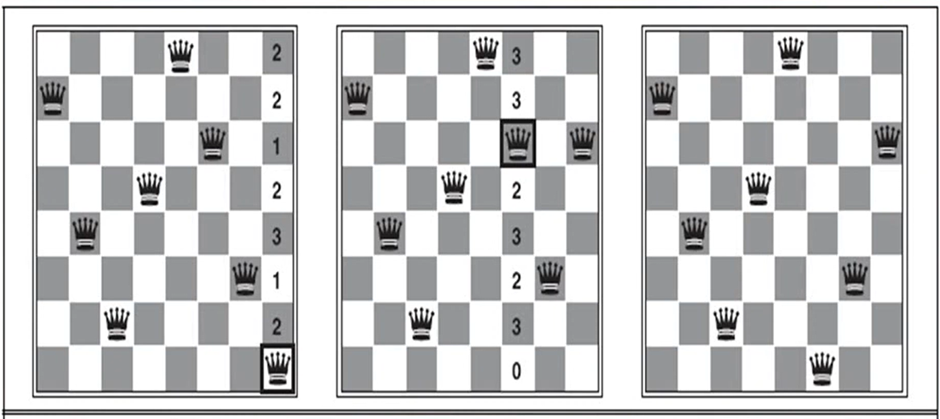
Figure 2: A 2 step solution using min-conflicts for an 8-queens problem. At each stage, a queen is choosen for reassignment in its column. The number of conflicts (in this case, the number of attacking queens) is shown in each square. The algorithm moves the queen to the min-conflicts square, breaking ties randomly.

Local Search for CSPs

Min-conflicts is surprisingly effective for many CSPs. Amazingly, on the n-queens problem, if you don't count the initial placement of queens, the run time of min-conflicts is roughly independent of problem size. It solves even the million-queens problem in an average of 50 steps. This remarkable observation was the stimulus leading to a great deal of research in the 1990s on local search and the distinction between easy and hard problems.
Roughly Speaking, n-queen is easy for local search because solutions are densely distributed throughout the state space. Min-conflicts also works well for hard problems.

About the Author

Silan Software is one of the India's leading provider of offline & online training for Java, Python, AI (Machine Learning, Deep Learning), Data Science, Software Development & many more emerging Technologies.

We provide Academic Training || Industrial Training || Corporate Training || Internship || Java || Python || AI using Python || Data Science etc