B+ trees are widely used index structures in relational database management systems (RDBMS) to efficiently organize and retrieve data. B+ trees are balanced tree structures that provide fast access to data records, especially for range queries and sorting operations. They are designed to minimize disk I/O and provide efficient search and insertion operations.

Here are the key features and characteristics of B+ trees:

1. Balanced Tree Structure:

The limitations of traditional binary search trees can be frustrating. Meet the B-Tree, the multi-talented data structure that can handle massive amounts of data with ease. When it comes to storing and searching large amounts of data, traditional binary search trees can become impractical due to their poor performance and high memory usage. B-Trees, also known as B-Tree or Balanced Tree, are a type of self-balancing tree that was specifically designed to overcome these limitations.
Unlike traditional binary search trees, B-Trees are characterized by the large number of keys that they can store in a single node, which is why they are also known as “large key” trees. Each node in a B-Tree can contain multiple keys, which allows the tree to have a larger branching factor and thus a shallower height. This shallow height leads to less disk I/O, which results in faster search and insertion operations. B-Trees are particularly well suited for storage systems that have slow, bulky data access such as hard drives, flash memory, and CD-ROMs.

B-Trees maintain balance by ensuring that each node has a minimum number of keys, so the tree is always balanced. This balance guarantees that the time complexity for operations such as insertion, deletion, and searching is always O(log n), regardless of the initial shape of the tree.

TIME COMPLEXITY-

Sr. No.	Algorithm	Time Complexity
1.	Search	O(log n)
2.	Insert	O(log n)
3.	Delete	O(log n)

Properties of B-Tree:

• All leaves are at the same level.
• B-Tree is defined by the term minimum degree ‘t‘. The value of ‘t‘ depends upon disk block size.
• Every node except the root must contain at least t-1 keys. The root may contain a minimum of 1 key.
• All nodes (including root) may contain at most (2*t – 1) keys.
• Number of children of a node is equal to the number of keys in it plus 1.
• All keys of a node are sorted in increasing order. The child between two keys k1 and k2 contains all keys in the range from k1 and k2.
• B-Tree grows and shrinks from the root which is unlike Binary Search Tree. Binary Search Trees grow downward and also shrink from downward.
• Like other balanced Binary Search Trees, the time complexity to search, insert and delete is O(log n).
• Insertion of a Node in B-Tree happens only at Leaf Node.

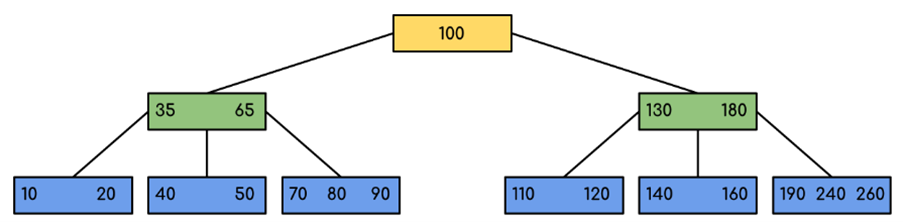
We can see in the above diagram that all the leaf nodes are at the same level and all non-leafs have no empty sub-tree and have keys one less than the number of their children.

Examples:

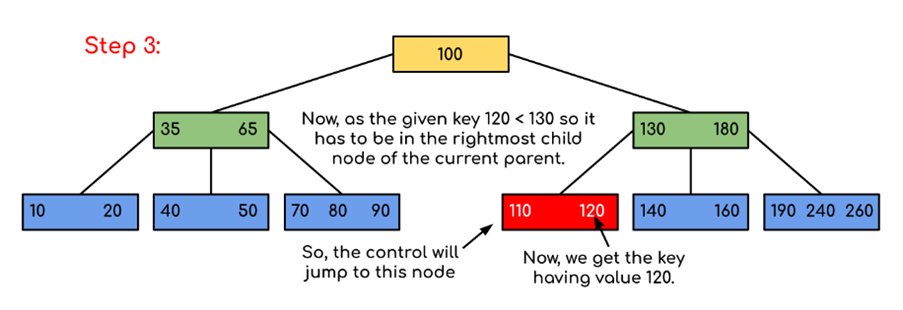
Input: Search 120 in the given B-Tree.

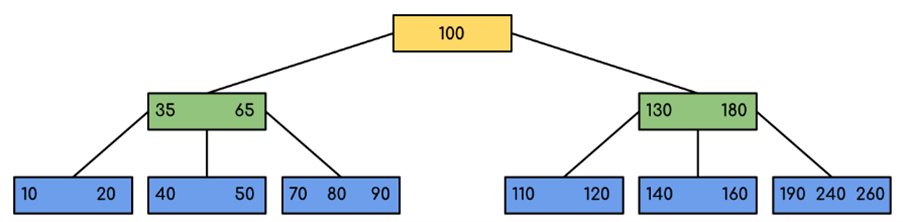
Solution:

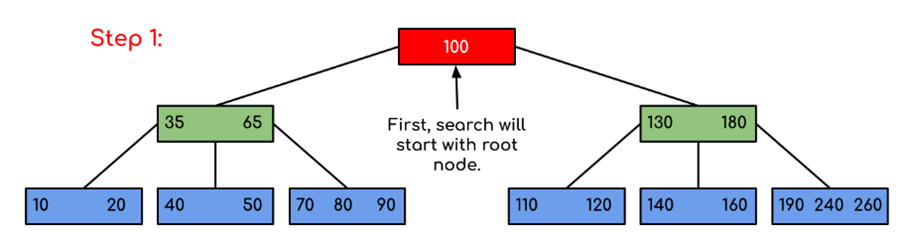
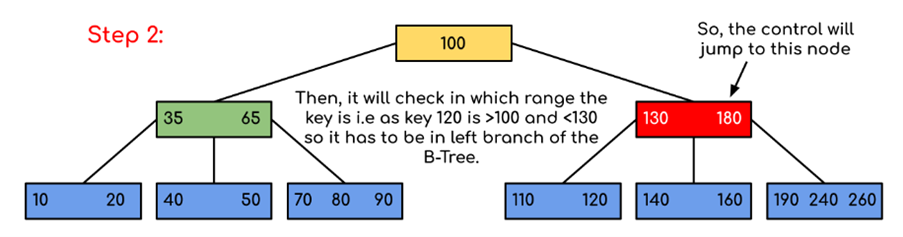
2. Leaf Nodes:

- The leaf nodes of a B+ tree contain index entries that point to the actual data records in the database.
- Leaf nodes are linked together in a linked list, allowing for efficient range queries and sequential access.
- The leaf nodes store the actual data records in sorted order based on the key values.

3. Internal Nodes:

- Internal nodes of the B+ tree contain a set of keys that divide the key ranges in the leaf nodes.
- These keys act as separators, guiding the traversal to the appropriate child node.
- The number of keys in an internal node is usually one less than the number of child pointers.

4. Fanout and Depth:

- The fanout of a B+ tree refers to the maximum number of child pointers or keys that can be stored in a node.
- A higher fanout value allows for more keys and pointers in each node, reducing the depth of the tree.
- The depth of a B+ tree is determined by the number of levels in the tree structure.

5. Split and Merge Operations:

- B+ trees have mechanisms to handle node splits and merges to maintain balance when inserting or deleting data.
- When a node becomes full, it is split into two nodes, and the median key is pushed up to the parent node.
- If a node becomes too empty due to deletions, it may be merged with a neighboring node to maintain balance.

B+ trees offer several benefits in RDBMS:

- Efficient range queries: B+ trees are particularly effective for range queries as the key-ordered leaf nodes allow for sequential scanning of records.

- Minimal disk I/O: B+ trees are designed to minimize disk accesses, reducing the time required to locate and retrieve data.

- Support for ordered data: B+ trees maintain the data records in sorted order, making them suitable for sorting operations without additional sorting overhead.

- Scalability: B+ trees can efficiently handle large datasets by adjusting the fanout and depth of the tree structure.

However, there are some considerations when using B+ trees:

- Overhead: B+ trees require additional storage space to maintain the index structure, especially when dealing with large datasets.

- Index Maintenance: Insertions and deletions in B+ trees require rebalancing operations, which can impact performance during updates.

- Key Selection: The effectiveness of B+ trees depends on the selectivity of the indexed attributes. If the selectivity is low, the benefits of the tree structure may be reduced.

B+ trees are widely used in RDBMS for indexing and are optimized for efficient data retrieval and query performance. The specific configuration of the B+ tree, such as the fanout and key selection, should be carefully chosen based on the characteristics of the data and the requirements of the database application.

About the Author

Silan Software is one of the India's leading provider of offline & online training for Java, Python, AI (Machine Learning, Deep Learning), Data Science, Software Development & many more emerging Technologies.

We provide Academic Training || Industrial Training || Corporate Training || Internship || Java || Python || AI using Python || Data Science etc